eriodic function
From Wikipedia, the free encyclopedia
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity.
Contents[hide] |
[edit] Definition
A function f is said to be periodic if
for all values of x. The constant P is called the period, and is required to be positive. A function with period P will repeat on intervals of length P, and these intervals are sometimes also referred to as periods.
Geometrically, a periodic function can be defined as a function whose graph exhibits translational symmetry. Specifically, a function f is periodic with period P if the graph of f is invariant under translation in the x-direction by a distance of P. This definition of periodic can be extended to other geometric shapes and patterns, such as periodic tessellations of the plane.
A function that is not periodic is called aperiodic.
[edit] Examples
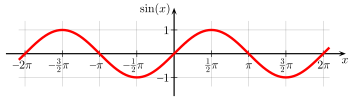
For example, the sine function is periodic with period 2π, since
for all values of x. This function repeats on intervals of length 2π (see the graph to the right).
Everyday examples are seen when the variable is time; for instance the hands of a clock or the phases of the moon show periodic behaviour. Periodic motion is motion in which the position(s) of the system are expressible as periodic functions, all with the same period.
For a function on the real numbers or on the integers, that means that the entire graph can be formed from copies of one particular portion, repeated at regular intervals.
A simple example of a periodic function is the function f that gives the "fractional part" of its argument. Its period is 1. In particular,
- f( 0.5 ) = f( 1.5 ) = f( 2.5 ) = ... = 0.5.
The graph of the function f is the sawtooth wave.
The trigonometric functions sine and cosine are common periodic functions, with period 2π (see the figure on the right). The subject of Fourier series investigates the idea that an 'arbitrary' periodic function is a sum of trigonometric functions with matching periods.
According to the definition above, some exotic functions, for example the Dirichlet function, are also periodic; in the case of Dirichlet function, any nonzero rational number is a period.
[edit] Properties
If a function f is periodic with period P, then for all x in the domain of f and all integers n,
- f(x + nP) = f(x).
If f(x) is a function with period P, then f(ax+b), where a is a positive constant, is periodic with period P/a. For example, f(x)=sinx has period 2π, therefore sin(5x) will have period 2π/5.
[edit] Double-periodic functions
A function whose domain is the complex numbers can have two incommensurate periods without being constant. The elliptic functions are such functions. ("Incommensurate" in this context means not real multiples of each other.)
[edit] Complex example
Using complex variables we have the common period function:
- ekix = coskx + isinkx
As you can see, since the cosine and sine functions are periodic, and the complex exponential above is made up of cosine/sine waves, then the above (actually Euler's formula) has the following property. If L is the period of the function then:
- L = 2π / k
[edit] Antiperiodic functions and other generalizations
One common generalization of periodic functions is that of antiperiodic functions. This is a function f such that f(x + P) = −f(x) for all x. (Thus, a P-antiperiodic function is a 2P-periodic function.)
A further generalization appears in the context of Bloch waves and Floquet theory, which govern the solution of various periodic differential equations. In this context, the solution (in one dimension) is typically a function of the form:
where k is a real or complex number (the Bloch wavevector or Floquet exponent). Functions of this form are sometimes called Bloch-periodic in this context. A periodic function is the special case k = 0, and an antiperiodic function is the special case k = π/P.
Periodic Time Functions
A periodic time function satisfies the expression
where n is a positive integer and T is the period of the periodic time function. The sinusoidal and sawtooth waveforms of Figure 8.1 are examples of periodic functions of time.
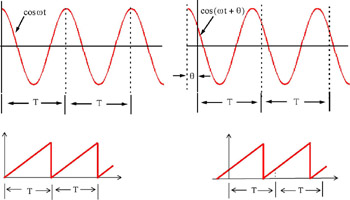
Figure 8.1: Examples of periodic functions of time
Other periodic functions of interest are the square and the triangular waveforms.
8.2 Average Values
The average value of any continuous function f (t) such as that shown in Figure 8.2 over an inter-val a ?t ?b,
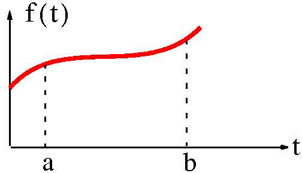
Figure 8.2: A continuous time function f(t)
is defined as
The average value of a periodic time function f(t) is defined as the average of the function over one period.
| |
Compute the average value of the sinusoid shown in Figure 8.3, where V p denotes the peak (maximum) value of the sinusoidal voltage.
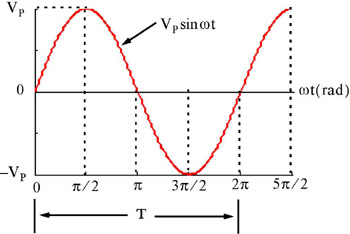
Figure 8.3: Waveform for Example 8.1
Solution:
By definition,

as expected since the net area of the positive and negative half cycles is zero.
| |
| |
Compute the average value of the half-wave rectification waveform shown in Figure 8.4.
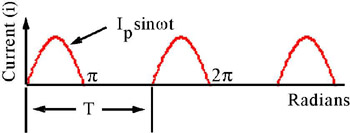
Figure 8.4: Waveform for Example 8.2
Solution:
This waveform is defined as

Then, its average value is found from



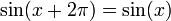

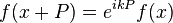
No comments:
Post a Comment